Calculus Basics Unveiled: A Comprehensive Guide to Understanding Core Concepts

Calculus, a branch of mathematics that studies continuous change, is pivotal in various fields, including engineering, physics, economics, and statistics. This guide provides a clear and comprehensive overview of calculus basics, focusing on its core concepts. Understanding these fundamentals will help you appreciate the broader applications of calculus and prepare you for more advanced topics.

1. Introduction to Calculus

Calculus is essentially divided into two main branches: differential calculus and integral calculus. Differential calculus focuses on the concept of a derivative, which represents the rate of change of a function. Integral calculus, on the other hand, deals with integrals, which represent the accumulation of quantities.

2. Key Concepts in Differential Calculus

a. Limits and Continuity

The limit of a function is the value that the function approaches as the input approaches a certain point. Limits are foundational to understanding derivatives and integrals. A function is continuous if its graph can be drawn without lifting your pencil, meaning there are no breaks or jumps.

b. Derivatives

The derivative of a function measures how the function’s output value changes as its input value changes. It’s formally defined as the limit of the average rate of change of the function over an interval as the interval approaches zero. In simpler terms, the derivative provides the slope of the tangent line to the function’s graph at a given point.

Example:

For the function f(x)=x2f(x) = x^2f(x)=x2, the derivative f′(x)=2xf'(x) = 2xf′(x)=2x. This means the slope of the tangent line to the graph of $f(x)$ at any point $x$ is $2x$.

c. Rules of Differentiation

Several rules simplify finding derivatives, including:

• Power Rule: ddx(xn)=nxn−1\frac{d}{dx}(x^n) = nx^{n-1}dxd​(xn)=nxn−1
• Product Rule: ddx(uv)=u′v+uv′\frac{d}{dx}(uv) = u’v + uv’dxd​(uv)=u′v+uv′
• Quotient Rule: ddx(uv)=u′v−uv′v2\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{u’v – uv’}{v^2}dxd​(vu​)=v2u′v−uv′​
• Chain Rule: ddx(f(g(x)))=f′(g(x))⋅g′(x)\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)dxd​(f(g(x)))=f′(g(x))⋅g′(x)

3. Key Concepts in Integral Calculus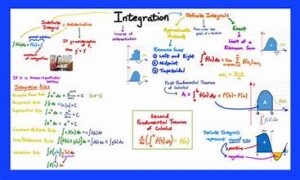

a. Indefinite Integrals

The indefinite integral, or antiderivative, of a function represents the family of functions whose derivative is the original function. It is denoted as $\int f(x)dx$ and includes a constant of integration $C$, because the derivative of a constant is zero.

Example:

For f(x)=x2f(x) = x^2f(x)=x2, the indefinite integral is ∫x2 dx=x33+C\int x^2 \, dx = \frac{x^3}{3} + C∫x2dx=3x3​+C.

b. Definite Integrals

Definite integrals represent the total accumulation of a quantity over an interval. The definite integral of a function from $a$ to $b$ is denoted as ∫abf(x) dx\int_a^b f(x) \, dx∫ab​f(x)dx and can be interpreted as the area under the curve of $f(x)$ from $a$ to $b$.

c. Fundamental Theorem of Calculus

This theorem links differentiation and integration, stating that if $F$ is an antiderivative of $f$ on an interval $[a,b]$, then:

∫abf(x) dx=F(b)−F(a)\int_a^b f(x) \, dx = F(b) – F(a)∫ab​f(x)dx=F(b)−F(a)

This theorem demonstrates that integration can be reversed by differentiation.

4. Applications of Calculus

Calculus has numerous applications across various disciplines:

• Physics: Calculus is used to describe motion, electricity, magnetism, and other physical phenomena.
• Engineering: It helps in analyzing and designing systems and structures, including everything from bridges to electrical circuits.
• Economics: Calculus is applied to model and predict economic behaviors, optimize production, and analyze cost functions.
• Biology: It aids in understanding population dynamics, growth rates, and other biological processes.

5. Common Challenges and Tips for Learning Calculus

a. Abstract Thinking

Calculus requires abstract thinking and understanding concepts that are not always visually intuitive. Practice visualizing problems and use graphical representations to aid understanding.

b. Practice Regularly

Calculus concepts build on each other. Regular practice and problem-solving will reinforce your understanding and help you master the material.

c. Seek Help When Needed

Don’t hesitate to ask for help from teachers, tutors, or online resources. Joining study groups or forums can also provide valuable insights and support.

Conclusion

Calculus is a fundamental area of mathematics with wide-ranging applications. By understanding its core concepts—limits, derivatives, integrals, and their rules—you’ll be well-equipped to tackle more complex problems and apply calculus to real-world scenarios. Embrace the challenge and enjoy the journey of learning this essential mathematical tool!