Understanding Prime Numbers: The Fascinating World of Mathematical Primes in 2024

Prime numbers have captivated mathematicians for centuries. As fundamental building blocks in the world of numbers, primes are essential for various applications, from cryptography to theoretical mathematics. In 2024, the study of prime numbers continues to offer new insights and challenges. This article delves into the nature of prime numbers, their significance, and recent advancements in prime number theory.

What Are Prime Numbers?

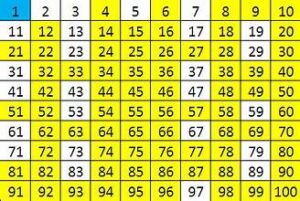
Prime numbers are defined as natural numbers greater than 1 that have no positive divisors other than 1 and themselves. For instance, 2, 3, 5, 7, and 11 are prime numbers. The number 2 is the only even prime number, while all other prime numbers are odd. This is because any even number greater than 2 can be divided by 2, making it a composite number rather than a prime.

The uniqueness of prime numbers lies in their indivisibility. They are the “atoms” of the number system, as every integer greater than 1 can be factored into primes, a property known as the Fundamental Theorem of Arithmetic.

The Significance of Prime Numbers

Prime numbers are not just mathematical curiosities; they play a crucial role in various fields:

1. Cryptography: Modern encryption techniques, such as RSA, rely on the difficulty of factoring large prime numbers. These methods secure online transactions and communications, making primes integral to cybersecurity.
2. Number Theory: Primes are central to number theory, a branch of mathematics focused on the properties and relationships of numbers. Concepts like prime distribution and the Riemann Hypothesis revolve around primes.
3. Algorithm Design: Efficient algorithms for prime testing and factorization are essential for various computational problems. The study of primes helps improve these algorithms, impacting fields ranging from computer science to engineering.

Recent Advances in Prime Number Theory

In 2024, researchers continue to explore the enigmatic properties of primes. Some notable advancements include:

1. Large Prime Discoveries: The quest for larger primes remains a central theme in number theory. The largest known prime as of 2024 is a Mersenne prime, which is a prime of the form 2p−12^p – 12p−1, where $p$ itself is a prime number. These primes are discovered using distributed computing projects like the Great Internet Mersenne Prime Search (GIMPS).
2. Prime Gaps: The study of gaps between successive prime numbers has yielded new insights. Recent research has provided improved bounds on the gaps between primes, contributing to our understanding of prime distribution and related conjectures.
3. Prime Numbers and Randomness: The connection between primes and randomness is a topic of ongoing research. Mathematical models explore how primes can be used to generate random sequences and their implications for fields like cryptography and statistical analysis.

Applications of Prime Numbers in Modern Technology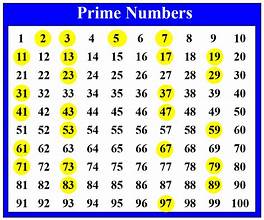

Prime numbers find applications beyond theoretical mathematics:

1. Digital Security: Cryptographic algorithms, including public-key cryptography, rely heavily on prime numbers. These algorithms ensure secure communications and data protection across various platforms, from online banking to email encryption.
2. Error Detection: In computer science, prime numbers are used in error-detection algorithms and hash functions. They help ensure data integrity and optimize performance in software systems.
3. Random Number Generation: Prime numbers are utilized in algorithms for generating pseudo-random numbers. These random number generators are crucial for simulations, gaming, and other applications requiring unpredictable sequences.

Challenges and Future Directions

The study of prime numbers continues to present challenges and open new avenues of research:

1. Distribution of Primes: Understanding how primes are distributed among natural numbers remains a central question. The Prime Number Theorem provides an approximation of the distribution, but exact results are still elusive.
2. Prime Number Algorithms: Developing more efficient algorithms for prime testing and factorization is an ongoing challenge. Advances in algorithms have the potential to impact both theoretical research and practical applications.
3. Primes in Higher Dimensions: Researchers are exploring the properties of primes in higher-dimensional spaces and their applications in fields such as coding theory and lattice cryptography.

Conclusion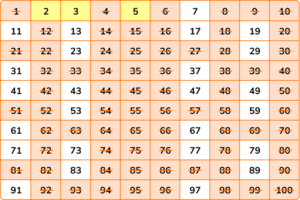

Prime numbers are a fundamental and fascinating aspect of mathematics. Their unique properties and applications extend far beyond basic arithmetic, influencing modern technology and cryptography. As we move through 2024, the study of primes continues to evolve, offering new discoveries and insights that shape our understanding of mathematics and its applications.