Understanding Quantum Numbers: Essential Insights for Students and Researchers in 2024

Quantum mechanics, the branch of physics that deals with the behavior of particles at the atomic and subatomic levels, is a field full of fascinating concepts and principles. Among these, quantum numbers are fundamental to understanding the arrangement and behavior of electrons within atoms. This article delves into the essentials of quantum numbers, their significance, and their applications, providing valuable insights for both students and researchers in 2024.

What Are Quantum Numbers?

Quantum numbers are values that describe the properties of atomic orbitals and the electrons within those orbitals. They are essential for understanding the electronic structure of atoms and molecules, and they play a critical role in quantum chemistry and physics. Each quantum number provides specific information about an electron’s position and energy, helping to determine the electron’s behavior and interaction with other particles.

The Four Types of Quantum Numbers

1. Principal Quantum Number (n):
   • Description: The principal quantum number denotes the main energy level or shell of an electron in an atom. It is a positive integer (1, 2, 3, …).
   • Significance: This number helps to determine the size and energy of the orbital. The higher the value of $n$, the larger the orbital and the higher its energy level.
   • Example: In a hydrogen atom, if an electron is in the third energy level, its principal quantum number $n$ is 3.
2. Azimuthal Quantum Number (l):
   • Description: The azimuthal quantum number, also known as the angular momentum quantum number, describes the shape of the orbital. It can have integer values from 0 to $n-1$.
   • Significance: This number determines the angular momentum of the electron and the shape of the orbital (s, p, d, f).
   • Example: For an electron in the second principal energy level ($n=2$), the possible values for $l$ are 0 (s-orbital) and 1 (p-orbital).
3. Magnetic Quantum Number (mₗ):
   • Description: The magnetic quantum number specifies the orientation of the orbital in space relative to the other orbitals. It can have integer values from $-l$ to $+l$.
   • Significance: This number affects the spatial distribution of electrons within an orbital.
   • Example: For a p-orbital ($l=1$), the magnetic quantum number mlmₗml​ can be -1, 0, or +1, corresponding to the three different orientations of the p-orbital.
4. Spin Quantum Number (mₛ):
   • Description: The spin quantum number indicates the intrinsic spin of the electron, which can be either +1/2 or -1/2.
   • Significance: Electron spin contributes to the magnetic properties of atoms and is crucial for the Pauli exclusion principle, which states that no two electrons in an atom can have the same set of quantum numbers.
   • Example: An electron with a spin quantum number of +1/2 is often referred to as “spin-up,” while -1/2 is “spin-down.”

The Role of Quantum Numbers in Atomic Structure

Quantum numbers are vital for determining the electron configuration of atoms, which in turn affects the chemical properties and reactivity of elements. The arrangement of electrons in different orbitals, governed by quantum numbers, determines how atoms bond and interact with each other.

1. Electron Configuration: Quantum numbers help in predicting the electron configuration of an atom, which describes how electrons are distributed among various orbitals. For instance, the electron configuration of oxygen (atomic number 8) is 1s² 2s² 2p⁴, where the quantum numbers dictate the distribution of its electrons in the s and p orbitals.
2. Periodic Table Organization: The periodic table’s layout reflects the arrangement of electrons in atomic orbitals. Elements are grouped into periods and groups based on their electron configurations, which are influenced by their quantum numbers.
3. Chemical Bonding: The quantum numbers also play a crucial role in chemical bonding. The way electrons are arranged in orbitals determines how atoms bond to form molecules. Understanding these arrangements helps chemists predict bonding patterns and molecular shapes.

Applications and Implications for Researchers

For researchers, quantum numbers are not just theoretical constructs but practical tools that have significant applications across various fields of science and technology.

1. Spectroscopy: Quantum numbers are used in spectroscopy to analyze the energy levels of electrons. By studying the spectral lines emitted or absorbed by atoms, researchers can infer information about electron transitions and the internal structure of atoms.
2. Quantum Computing: In the field of quantum computing, quantum numbers help in understanding and manipulating quantum states. Quantum bits or qubits, the fundamental units of quantum computers, rely on principles of quantum mechanics, including quantum numbers, to perform complex computations.
3. Material Science: Quantum numbers are essential in material science for designing and understanding new materials. The electronic properties of materials, such as their conductivity and magnetism, are influenced by the quantum numbers of the electrons in the material’s atoms.
4. Molecular Biology: In molecular biology, quantum numbers help in understanding the electronic interactions between molecules and their biological functions. This knowledge is crucial for designing drugs and studying biological processes at the molecular level.

Educational Resources and Tools for Learning

For students and researchers looking to deepen their understanding of quantum numbers, various resources and tools are available:

1. Textbooks and Academic Journals: Books like “Principles of Quantum Mechanics” by R. Shankar and “Quantum Chemistry” by Ira N. Levine provide comprehensive explanations of quantum numbers and their applications.
2. Online Courses: Platforms like Coursera and edX offer courses on quantum mechanics and quantum chemistry that cover quantum numbers in detail.
3. Simulation Software: Tools such as MATLAB and Quantum Development Kit (QDK) allow users to simulate quantum systems and visualize the effects of quantum numbers on electron behavior.
4. Interactive Websites: Websites like Khan Academy and HyperPhysics offer interactive tutorials and visual aids to help students grasp the concepts of quantum numbers and their significance.

Conclusion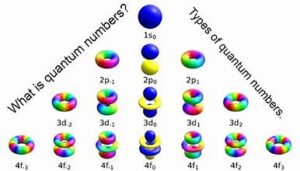

Quantum numbers are a cornerstone of quantum mechanics, providing critical insights into the behavior and arrangement of electrons in atoms. Understanding these numbers is essential for students and researchers across various scientific disciplines, from chemistry and physics to material science and quantum computing. As we advance into 2024, mastering the concepts of quantum numbers will continue to be crucial for exploring the complexities of the atomic world and leveraging this knowledge in practical applications. Whether you’re a student delving into quantum mechanics or a researcher pushing the boundaries of science and technology, a solid grasp of quantum numbers will enhance your understanding and contribute to your success in the field.