Algebraic equations are fundamental to many fields of mathematics, but their role in machine learning (ML) and artificial intelligence (AI) is particularly crucial. These equations provide the backbone for algorithms that drive modern AI applications, from simple data analysis to complex predictive models. Understanding how algebraic equations are employed in these domains can offer valuable insights into their functionality and applications. This article explores the significance of algebraic equations in machine learning and AI, highlighting key concepts and practical implementations.
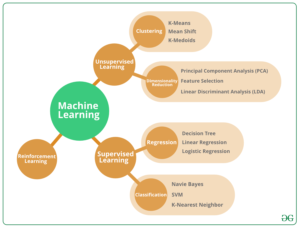
1. Understanding Algebraic Equations in ML and AI
Algebraic equations are mathematical statements that express the equality between two expressions. In machine learning and AI, these equations are used to model relationships between variables and to develop algorithms that can make predictions or decisions based on data.
**a. Linear Algebra: A Key Component
Linear algebra, a branch of algebra involving vectors and matrices, plays a crucial role in machine learning. Algorithms often rely on matrix operations to handle and process large datasets efficiently. For instance, linear regression, a fundamental ML algorithm, uses algebraic equations to find the best-fitting line through a set of data points by minimizing the sum of the squared differences between observed and predicted values.
**b. Polynomial Equations and Non-Linear Models
In addition to linear equations, polynomial equations are employed in machine learning to capture more complex relationships. Non-linear models, such as polynomial regression or support vector machines with non-linear kernels, use algebraic equations to create decision boundaries that are not necessarily straight lines, allowing for more sophisticated data fitting and classification.
2. Applications of Algebraic Equations in Machine Learning
**a. Optimization Algorithms
Optimization is a key process in machine learning, where algebraic equations are used to minimize or maximize certain functions. For example, gradient descent, a popular optimization algorithm, utilizes derivatives (which are algebraic expressions) to iteratively adjust the parameters of a model in order to find the optimal solution.
**b. Neural Networks
Neural networks, a cornerstone of deep learning, rely heavily on algebraic equations. These networks consist of layers of interconnected nodes, each performing linear transformations followed by non-linear activations. The training process of neural networks involves solving complex systems of algebraic equations to adjust weights and biases, enabling the network to learn from data.
**c. Dimensionality Reduction
Techniques such as Principal Component Analysis (PCA) use algebraic equations to reduce the dimensionality of datasets while preserving as much variance as possible. PCA involves solving eigenvalue problems and performing matrix decompositions to transform data into a lower-dimensional space, which helps in visualization and computational efficiency.
3. Insights into Algebraic Equations and AI
**a. Scalability and Efficiency
Algebraic equations enable machine learning models to handle large-scale data efficiently. Matrix operations, such as those used in deep learning frameworks, allow for the parallel processing of data, which significantly speeds up computations and makes it feasible to work with vast amounts of information.
**b. Accuracy and Precision
The precision of machine learning models often hinges on the accuracy of algebraic equations used in algorithms. By carefully designing and tuning these equations, researchers and practitioners can enhance the performance of models, improving their ability to make accurate predictions and decisions.
**c. Interdisciplinary Applications
The application of algebraic equations in AI extends beyond traditional machine learning. They are also crucial in fields such as computer vision, natural language processing, and robotics. For instance, algebraic transformations are used in image processing to detect edges and patterns, while in natural language processing, algebraic techniques are applied to understand and generate human language.
4. Challenges and Future Directions
**a. Complexity of Equations
As AI technologies advance, the algebraic equations involved in machine learning models can become increasingly complex. Researchers face the challenge of developing efficient algorithms to solve these equations while ensuring that models remain interpretable and manageable.
**b. Integration with Other Technologies
Future advancements in AI may involve integrating algebraic equations with other technologies, such as quantum computing. This integration could potentially revolutionize how equations are solved and applied, leading to more powerful and efficient machine learning models.
**c. Ethical Considerations
The use of algebraic equations in AI also brings ethical considerations. Ensuring that algorithms do not perpetuate biases or make unfair decisions is an ongoing concern. Developing transparent and fair algorithms requires a deep understanding of the algebraic foundations and their implications in real-world applications.
Conclusion
Algebraic equations are integral to the functioning of machine learning and AI systems. They provide the mathematical foundation for a wide range of algorithms, from optimization and neural networks to dimensionality reduction. Understanding their role not only enhances our grasp of these technologies but also guides the development of more effective and efficient models. As AI continues to evolve, the application and complexity of algebraic equations will likely advance, presenting new opportunities and challenges in the field.



